
CBL award
January 2022: I am very pleased to have been granted within the call for proposals on challenge-based implementation at the UT, in order to accelerate the adoption of CBL within the UT.

January 2022: I am very pleased to have been granted within the call for proposals on challenge-based implementation at the UT, in order to accelerate the adoption of CBL within the UT.
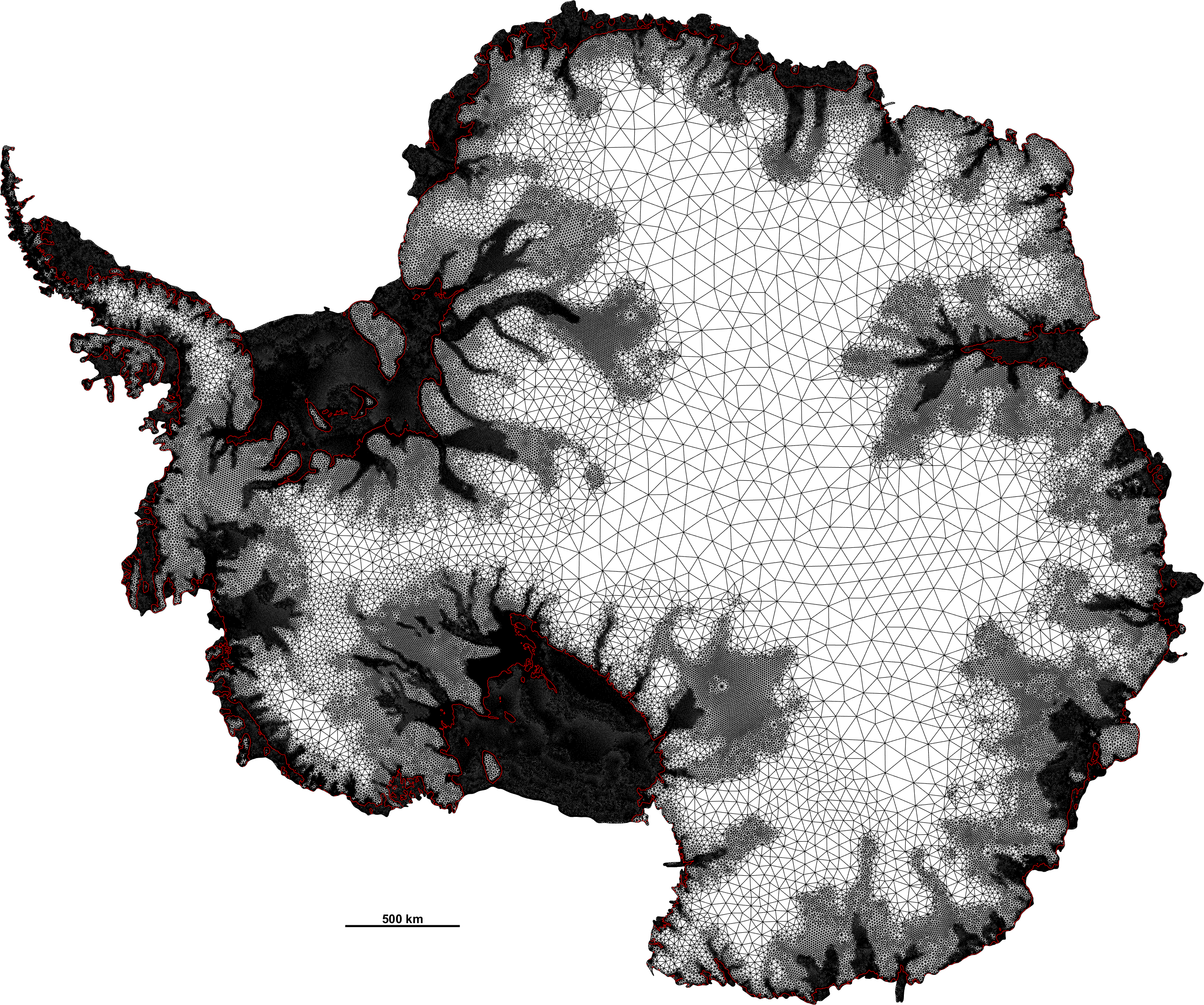
The finite element method (FEM) is the most widely used method for solving partial differential equations numerically. These equations arise in engineering and mathematical modelling. The range of the applications is immense, although typical applications include solid and fluid mechanics, electromagnetism or biology.
The finite element method is based on a variational equation, for which we will first develop some analytical insight. We will then consider appropriate discrete subspaces (the finite element subspaces) in which we can solve the variational equation. This leads to several algorithms for which the error analysis will be discussed. A further focus will be the design of a corresponding error estimator and its use in an adaptive strategy.
This course has, therefore, two aims:
- Expose the student to the variational framework on which the finite element method is based and enrich the students' knowledge on numerical analysis.
- Practicing programming using Matlab with emphasis on efficiency and correctness.
After this course, the student has the ability to implement the finite element method for a given problem efficiently and reliably.
Thanks to an increase in computing power the opportunities for understanding and solving complex problems in engineering applications, life sciences, environmental issues, urban systems, and finance have rapidly grown in recent decades and thus advanced the corresponding research area Scientific Computing. Typical tasks are modelling the respective problem, developing a numerical method for the approximation, and implementing the respective algorithms on a computer.
In the course Scientific Computing we will look at several (real-world) applications such as determining the eigenfrequencies of a bridge or determining the page rank of a webpage, model them and discuss and implement the respective algorithms to solve the problem in a possibly simplified setting. As solving linear system of equations is a task which appears in many different contexts we start with this topic. As very many phenomena such as the deformation of structures, heat conduction, fluid flow and so on can be modelled well by partial differential equations (PDEs), we discuss PDEs in a simple one-dimensional setting, where we also discuss some modelling aspects and introduce Sobolev spaces. Since the finite element method is by far the most common method to compute an approximation of the solution of an PDE we introduce the Finite Element method still in the simple one-dimensional setting and prove convergence of the approximation towards the solution.
Large-scale eigenvalue problems can be encountered for instance when analyzing social networks or when determining eigenfrequencies of large structures. Therefore, we discuss large scale eigenvalue solvers next. As specific applications we consider PageRank and the Finite Element approximation of the Helmholtz equation in detail. Next, we discuss algorithms from randomized numerical linear algebra which are highly popular in (big-)data analytics and become also more important in numerical simulations. Providing subsequently a brief introduction to deep neural networks with a focus on randomized methods for solving optimization problems gives students basic knowledge about ever more used deep nets that have many different applications. We close the course by considering mixed-integer nonlinear programming problems (MINLP), including linearization-based (outer) approximations and nonlinear branch-and-bound, as well as using solver technology for the practical solution of MINLPs.